Dr. Boyd: It’s more important to consider aerators’ impact on soil erosion

I often receive questions about what effect various phenomena or treatments have in aquaculture. Some of these questions must be answered as follows: Yes, there is an effect, but the effect is not great enough to be beneficial or detrimental.
Some examples: Will putting lighting around a pond result in more dissolved oxygen at night? Does rain falling into a pond increase the dissolved oxygen concentration? Will applying a small amount of zeolite weekly lessen ammonia concentration? Does lime increase the temperature of pond water? Should aerators be positioned to create a rotation of circulation in harmony with the Coriolis force?
Had I maintained a list of the questions about true but inconsequential – at least to aquaculture management – phenomena or treatments, the most frequently asked one would no doubt be about the best rotation direction for aerator-induced pond water circulation.
But this question has been asked with only slightly more frequency than the lime-pond water temperature question. These two questions are so common that I believe each is deserving of a column, and the present column will be devoted to aerator position and the Coriolis force (or Coriolis effect).
As you may have surmised, the answer to the aerator placement-Coriolis question is that the effect occurs, but it is of no importance in pond management. I have had little success convincing people that it does not matter whether aerators are positioned to follow the direction of the Coriolis effect.
My stock response is this: Although this effect is important for determining circulation and direction of travel of large air and water masses, it is not important in a small-scale system such as a pond. Most seem not to be impressed, so I will try a longer answer.
Coriolis physics
The physics of the Coriolis force are quite complex. According to Newton’s second law of motion, the acceleration of an object as a result of a net force is directly proportional to the magnitude of the net force and in the same direction. However, Newton’s second law is based on an inertial (non-accelerated) system, i.e., the object is in a stationary frame. However, the earth’s rotation causes objects at rest to have centripetal acceleration.
The Coriolis force is necessary to explain motions in a rotating coordinate frame relative to them being observed in a stationary coordinate frame. The rotating earth causes straight lines to appear as curved lines. The Coriolis force is the force that would be required to cause the curved lines in an inertial frame of reference.
A simple illustration of Coriolis force will be provided with aid of Fig. 1. Consider a helicopter hovering in place above the equator. The helicopter is motionless with respect to a reference point on the earth’s surface, but both the helicopter and the earth’s surface are moving from west to east at the speed of the earth’s rotation (1,670 km/hr. at the equator).
Suppose that the helicopter starts to move due north. The circumference of the earth decreases with distance north or south of the equator (Fig. 1). As a result, the speed of rotation of a point on the earth’s surface decreases progressively with distance north or south of the equator. Although the helicopter moves north from the equator, it retains a west to east velocity of 1,670 km/hr. But, as the helicopter moves north, the ground below rotates at a slower speed than it did at the equator because of the decreasing circumference of the earth.
As a result, the helicopter will deflect to the right with respect to a point on the ground, because as it moves north of the equator, its west-to-east velocity exceeds the velocity of a point on the ground. The opposite effect will occur if the helicopter travels directly south from the equator – it will deflect to the left.
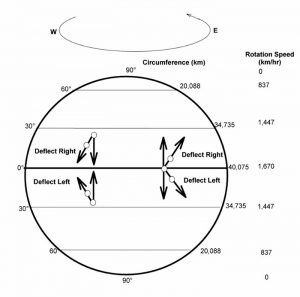
The Coriolis effect is widely understood to affect air masses and ocean currents. It causes massive storms to rotate clockwise in the northern hemisphere and counterclockwise in the southern hemisphere. Moreover, storms deflect instead of travelling in straight lines, and the deflection is right in the northern hemisphere and left in the southern hemisphere. The Coriolis force also causes ocean currents to deflect and rotate clockwise in the northern hemisphere and vice versa.
Migrating birds and airplane pilots must adjust for the Coriolis effect to arrive at their intended destinations. Artillery must be aimed in a way to compensate for the Coriolis effect or projectiles will not strike their intended targets. Of course, the effect of the Coriolis depends upon the distance and speed of a travelling object.
Rossby number
The Rossby number is used to compare the effect of the Coriolis force with the effect of inertial forces (those considered in Newton’s second law of motion). The Rossby number is the ratio of the velocity of the flow field (air or water) to the product of the distance (length) of the flow field and the angular velocity.
The earth’s angular velocity (rotation speed) is expressed as radians per day or 2p/24. If the Rossby number is distinctly greater than 1, the Coriolis force is negligible. If the Rossby number is distinctly less than 1, inertial forces are negligible and the Coriolis force is more important. At Rossby numbers near 1, both inertial and Coriolis forces are important.
For a weather front moving at a speed of 20 km/h over a distance of 1,000 km, the Rossby number would be 0.076, indicating that the Coriolis effect is very important in the direction of forward movement by the air mass. Of course, the Coriolis effect also causes air masses to circulate in a clockwise or counterclockwise direction.
The velocity of water in an aerated shrimp pond would be about 20 cm/sec (0.72 km/hr.), and the distance across a shrimp pond would usually not exceed 100 m (0.1 km). The Rossby number would be 27.5, suggesting the Coriolis force will have a negligible effect on water circulation in an aquaculture pond. If the pond was larger – say a 250-meter flow distance – the Rossby number would still be large (11.0) and inertial forces would overshadow the Coriolis effect. Positioning aerators to oppose the Coriolis effect – counterclockwise circulation in the northern hemisphere and clockwise flow in the southern hemisphere – would not affect the efficiency of aerators in inducing water circulation.

Perspectives
The most important issue with mechanical aeration is to provide a sufficient amount to maintain adequate dissolved oxygen concentration (3-4 mg/L minimum). It also is important to position aerators so that the water currents that they produce do not impinge directly on embankments and cause serious erosion.
Finally, I want to put another common belief to rest. The water in bathtubs, sinks and commode bowls circulates in the direction that it enters these vessels instead of in a direction determined by the Coriolis force – the scale is just too small to be affected by the Coriolis.
Now that you've reached the end of the article ...
… please consider supporting GSA’s mission to advance responsible seafood practices through education, advocacy and third-party assurances. The Advocate aims to document the evolution of responsible seafood practices and share the expansive knowledge of our vast network of contributors.
By becoming a Global Seafood Alliance member, you’re ensuring that all of the pre-competitive work we do through member benefits, resources and events can continue. Individual membership costs just $50 a year.
Not a GSA member? Join us.
Author
-

Claude E. Boyd, Ph.D.
School of Fisheries, Aquaculture and Aquatic Sciences
Auburn University
Auburn, AL 36830 USA[117,100,101,46,110,114,117,98,117,97,64,49,101,99,100,121,111,98]
Related Posts

Innovation & Investment
After half a century, Auburn’s Claude Boyd to ‘retire’
Friends, colleagues and former students of longtime Auburn University Professor Claude E. Boyd, Ph.D., don’t expect the Mississippi native to slow down, despite the quiet announcement of his retirement earlier this month. The 50-year veteran researcher’s career has been truly extraordinary.

Health & Welfare
Decomposition and accumulation of organic matter in ponds
Aquaculture ponds accumulate organic matter from organic fertilizer, remains of microorganisms produced within the pond, feces of the culture animals and uneaten feed. Claude E. Boyd, Ph.D., details the leading organic matter management practices, and says that the accumulation of organic matter is often not as great as believed.

Responsibility
Efficiency of mechanical aeration
Although relatively expensive, mechanical aeration increases production. Asian-style paddlewheel aerators are widely used but are inefficient. Testing has led to more efficient designs that are now widely used in U.S. catfish and shrimp ponds.

Responsibility
Reviewing the ‘near-magical’ properties of water
Understanding the hydrologic cycle, water’s unique physical properties and their behavior in aquaculture systems – phases, humidity, saturation, stratification, light reflection and refraction – is pertinent to properly manage water quality in production systems, according to world-renowned expert Dr. Claude Boyd.


